Математическая модель рынка. Метод определения "справедливых" цен

Здравствуйте, дамы и господа!

Думаю, что всем хочется покупать финансовые инструменты подешевле, а продавать подороже. Реакция участников торгов на новости, как правило, непропорциональна и чрезмерна: пессимисты склонны недооценивать актив, а оптимисты, напротив, его переоценивают. В определении текущих «перекупленности» или «перепроданности» активов теханализ помогает мало. Предположим, что золото подорожало и его цена в USD на историческом максимуме. Означает ли это, что его цена «несправедливо» завышена? Совсем необязательно. Она может вырасти, например, если девальвировался доллар, и тогда самая высокая его цена остается справедливой и обоснованной. А если ВСЕ основные валюты постепенно теряют покупательскую способность? Тогда девальвация USD может быть незаметна, но цена золота (и многих других активов) «справедливо» вырастет из-за инфляции.

Несколько перефразируя Дядю Федора, можно сказать, что чтобы купить что-нибудь ненужное, инвесторам надо продать что-нибудь ненужное. Деньги «перетекают» из акций в золото и облигации, из драгметаллов в кеш, из одной валюты в другую (и обратно). Поэтому для «справедливой» оценки актива его цену нужно сравнивать с ценами максимально широкого набора финансовых инструментов и построить математическую модель взаимных зависимостей их стоимости.

Чтобы эти зависимости были устойчивыми, инструменты должны быть достаточно ликвидными, тогда влияние на их цены случайных факторов (заявок покупателей и продавцов) будет неслучайным в соответствии с Законом больших чисел.

Для своей модели я выбрал следующие десять: евро, франк, йена, канадский доллар, золото, серебро, медь, фьючерс на S&P, нефть Brent, природный газ. В датафрейм включил также в качестве одного из факторов, влияющих на цены, даты наблюдений в целочисленном формате (как в Excel) для учета влияния долгосрочных тенденций и инфляции.

Данные взял из MT4 (Forex Club) с 01.01.2014 по настоящее время (D1, 1483 строки):



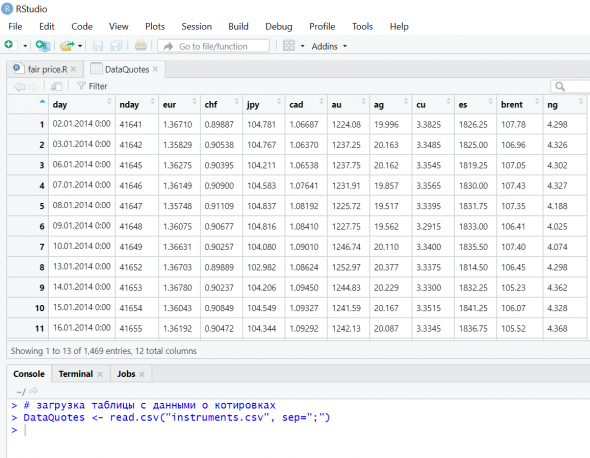
Для оценки эффективности своей модели я решил сравнить ее результат с двумя традиционными моделями — простой трехслойной нейросетью и многофакторной линейной регрессионной. Исходные данные я нормализовал, разделив каждое значение в столбце датафрейма на максимальное значение:



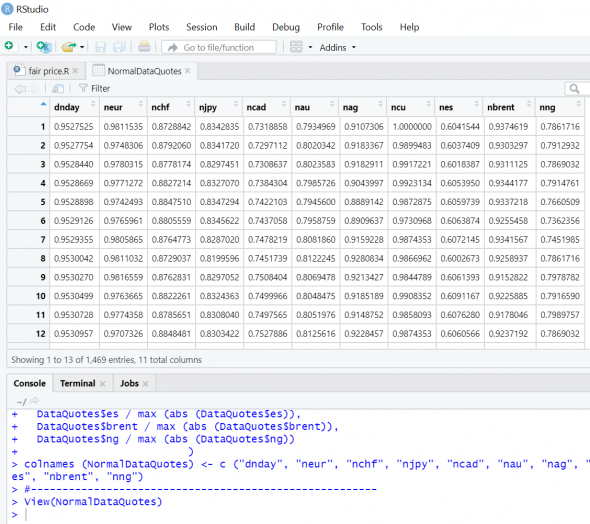
Для каждой строки датафрейма сгенерил в столбце «Random» случайное число. Для обучающей выборки взял значения, меньшие 0.8 по модулю, а для тестовой – все остальные. Получилось 1164 и 319 строк соответственно.



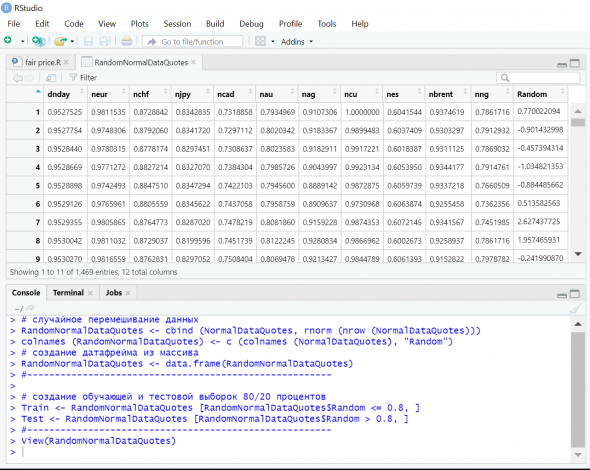
По данным обучающей выборки создал три модели для расчета «справедливой» цены евро: с помощью нейросети, линейную регрессионную и «мою модель». Рассчитанные моделями значения EUR по данным тестовой выборки внес в таблицу, добавив три столбца «PrNN», «PrLM» и «PrMM»:



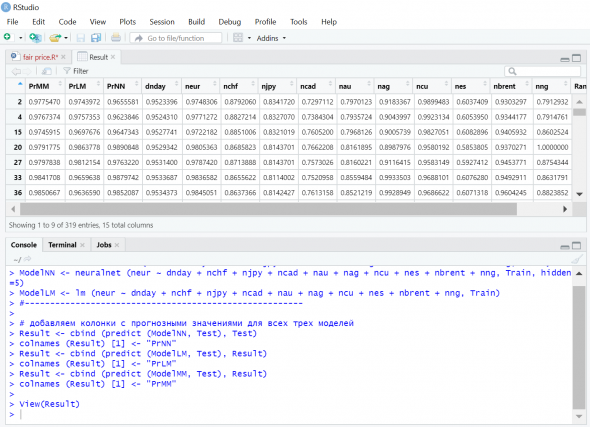
Схема нейросети:



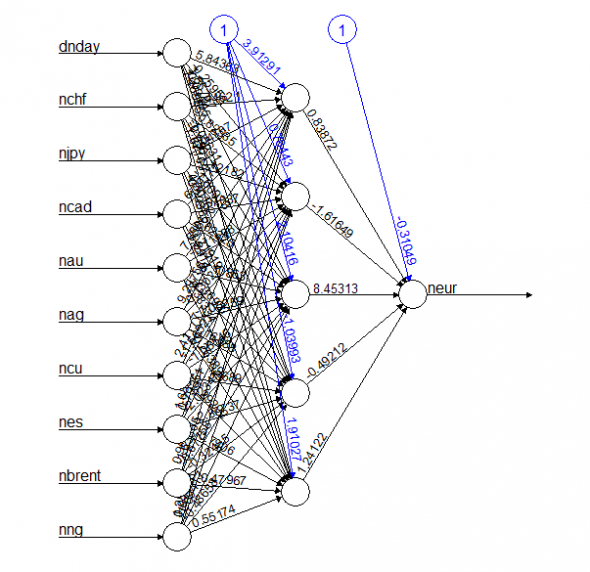
Для сравнения качества моделей рассчитал RMSE (Root mean square error):



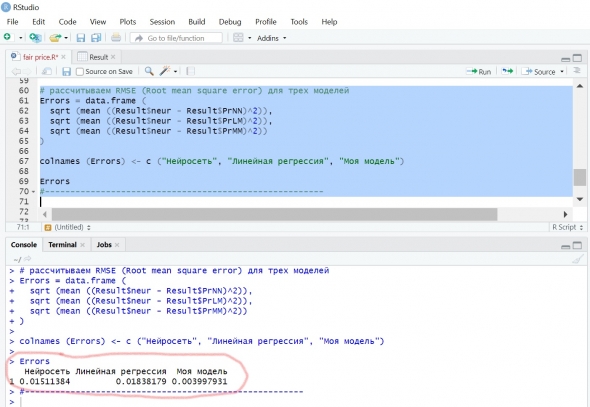
Как видно на скриншоте выше, традиционные модели, нейросеть и линейная регрессионная, дали дали близкую по величине ошибку – чуть более полутора процентов. Причем, качество регрессионной модели высокое: коэффициент детерминированности R2 = 0.92, что примерно соответствует коэффициенту корреляции 0.85. Распределение ошибок – нормальное, проверял тестом Шапиро-Уилка и критерием Пирсона («хи-квадрат»):




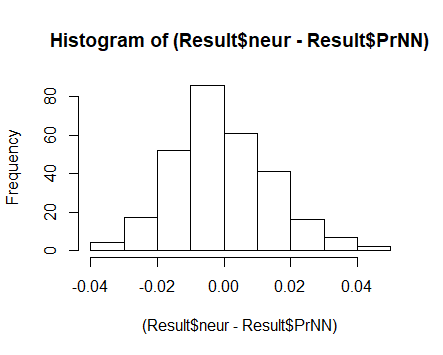
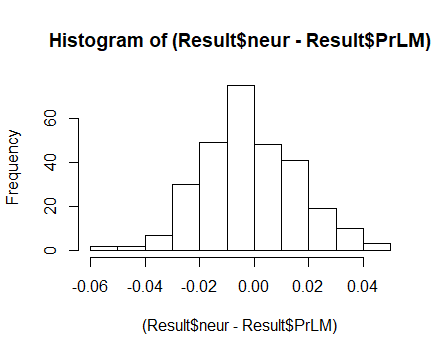
Но какой результат дал алгоритм «Моей модели»! Ошибка менее 0.4% (!).




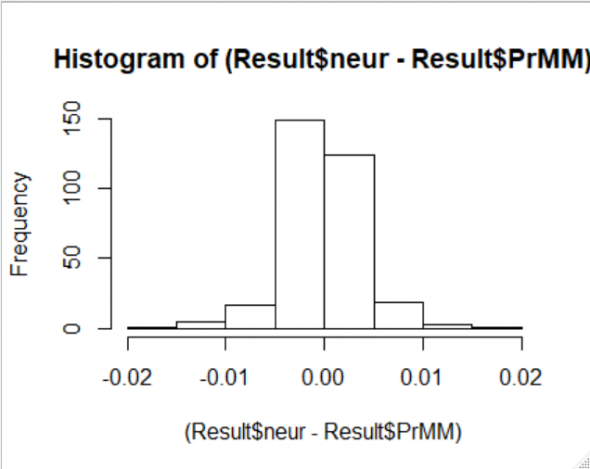
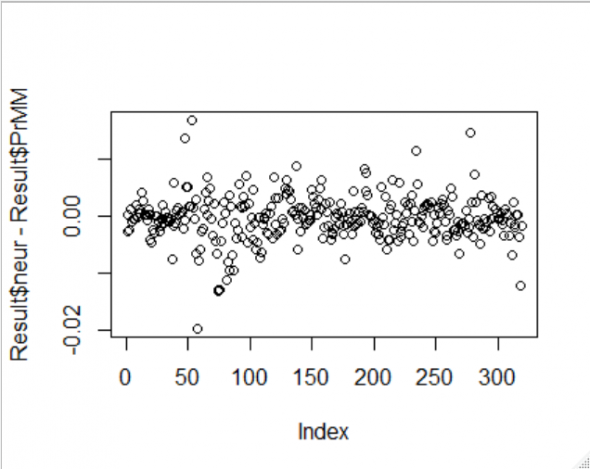
Причина вот в чем: на качество модели, особенно регрессионной, большое влияние оказывают так называемые «выбросы» — значения прогнозируемого показателя, существенно отклоняющиеся от средних. Они вызывают отклонение линии регрессии от области, в которой сосредоточена большая часть значений показателя, что ухудшает способность модели прогнозировать показатель. Обычно выборку разными способами очищают от «выбросов», но я счел это неприемлемым в данном конкретном случае, так как отсутствуют четкие критерии определения «выбросов» и существует риск получить в результате выборку, не отражающую свойства генеральной совокупности.

Я, как когда-то один из классиков М-Л, «пошел другим путем»: я создал из выборки в 1483 строки данных 500 «субвыборок», в которые случайным образом включал 90% данных. В исключенные 10% данных иногда попадали «выбросы» и построенная по такой субвыборке модель становилась качественнее. Построив 500 регрессионных моделей и рассчитав 500 значений моделируемого показателя, я принимал к в качестве прогнозного его значения среднее арифметическое из 500 смоделированных значений. Результат работы такого алгоритма приведен выше.

Так как распределение «ошибок» нормальное, то с вероятностью 67% текущее фактическое значение цены финансового инструмента будет находиться в интервале +-RMSE, а с вероятностью 95% в интервале +-2*RMSE.

Модель вполне годится для расчета «справедливых» цен финансовых инструментов с приемлемой точностью. Можно использовать в торговле: если текущая цена выше (ниже) рассчитанных по модели значения «справедливой» цены и разница превышает два RMSE – нужно продавать (покупать). Можно также анализировать динамику «справедливой цены».

С помощью предложенного метода также можно определять «справедливые» цены компаний по показателям ФХД, но с учетом ситуации на рынке – «аппетита к риску», стоимости валюты, в которой акция номинирована, цен на сырье и т.п.

Профита всем!

Если статья вам понравилась, жмите сюда,

А если нет, то сюда.

Потрясающе!Фантастика! ))

А как это помогает при торговле?))